如何评价一个算法的好坏

首先，这个算法必须是正确的

其次，好的算法应该是友好的，便于人们理解和交流，并且是机器可执行的。

这个算法还需要足够健壮，即当输入的数据非法或不合理时，也能适当的做出正确的反应或进行相应的处理

最后它还必须拥有高效率和低存储量要求。

也就是所谓的时间复杂度和空间复杂度

1.时间复杂度

定义:在计算机科学中,算法的时间复杂度是一个函数,他定量描述了该算法的运行时间.一个算法执行所耗费的时间,从理论上讲,只有你把你的程序放机器上跑起来,才能知道.然而我们有一套时间复杂度的分析方式.一个算法所花费的时间与其中语句的执行次数成正比例.算法中的基本操作的执行次数,为算法的时间复杂度.

2.时间复杂度为什么不使用时间来衡量而使用基本语句的运行次数来衡量？

算法的执行时间依赖于具体的软硬件环境，所以，不能用执行时间的长短来衡量算法的时间复杂度，而要通过基本语句执行次数的数量级来衡量。

3.时间复杂度的O渐进表示法 (Big O notation)

是用于描述函数渐进行为的数学符号.

大O阶方法推导:计算基本语句的执行次数的数量级；　只需计算基本语句执行次数的数量级，这就意味着只要保证基本语句执行次数的函数中的最高次幂正确即可，可以忽略所有低次幂和最高次幂的系数。这样能够简化算法分析，并且使注意力集中在最重要的一点上：增长率。　如果算法中包含嵌套的循环，则基本语句通常是最内层的循环体，如果算法中包含并列的循环，则将并列循环的时间复杂度相加。例如：　for (i=1; i<=n; i++)　　x++;　　　　for (i=1; i<=n; i++)　　for (j=1; j<=n; j++)　　x++;　第一个for循环的时间复杂度为Ο(n)，第二个for循环的时间复杂度为Ο(n2)，则整个算法的时间复杂度为Ο(n+n2)=Ο(n2)。

4.时间复杂度的:最优、平均、最差情况，为什么时间复杂度看的是最差情况？

最差情况下的复杂度是所有可能的输入数据所消耗的最大资源，如果最差情况下的复杂度符合我们的要求，我们就可以保证所有的情况下都不会有问题。

某些算法经常遇到最差情况。比如一个查找算法，经常需要查找一个不存在的值。也许你觉得平均情况下的复杂度更吸引你，可是平均情况也有几点问题。第一，难计算，多数算法的最差情况下的复杂度要比平均情况下的容易计算的多，第二，有很多算法的平均情况和最差情况的复杂度是一样的. 第三，什么才是真正的平均情况？如果你假设所有可能的输入数据出现的概率是一样的话，也是不合理的。其实多数情况是不一样的。而且输入数据的分布函数很可能是你没法知道。考虑最好情况的复杂度更是没有意义。

5.如何求解：二分查找、递归求阶乘、递归斐波那契的时间复杂度？

二分查找:通过折纸查找求解时间复杂度为O(logN);递归求阶乘:数基本操作递归N次得到时间复杂度为O(N);递归斐波那契:分析得出基本操作递归了2N次,时间复杂度为O(2N);

6.什么是空间复杂度？

空间复杂度是对一个算法在运行过程中临时占用存储空间大小的度量.空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数.空间复杂度计算规则基本跟时间复杂度类似,也使用大O渐进法表示.

7.如何求空间复杂度？ 普通函数&递归函数

一个算法的空间复杂度只考虑在运行过程中为局部变量分配的存储空间的大小，它包括为参数表中形参变量分配的存储空间和为在函数体中定义的局部变量分配的存储空间两个部分。若一个算法为 递归算法，其空间复杂度为递归所使用的堆栈空间的大小，它等于一次调用所分配的临时存储空间的大小乘以被调用的次数(即为递归调用的次数加1，这个1表示开始进行的一次非递归调用)。算法的空间复杂度一般也以数量级的形式给出。如当一个算法的空间复杂度为一个常量，即不随被处理数据量n的大小而改变时，可表示为O(1)；当一个算法的空间复杂度与以2为底的n的对数成正比时，可表示为O(log2n)；当一个算法的空间复杂度与n成线性比例关系时，可表示为O(n).若形参为数组，则只需要为它分配一个存储由实参传送来的一个地址指针的空间，即一个机器字长空间；若形参为引用方式，则也只需要为其分配存储一个地址的空间，用它来存储对应实参变量的地址，以便由系统自动引用实参变量。

8. 分析递归斐波那契数列的：时间、空间复杂度，并对其进行优化，伪递归优化—>循环优化long long Fib(int N) {if (N < 3)return 1;return Fib(N - 1) + Fib(N - 2);}普通递归实现的斐波那契数列:时间复杂度:O(2^n)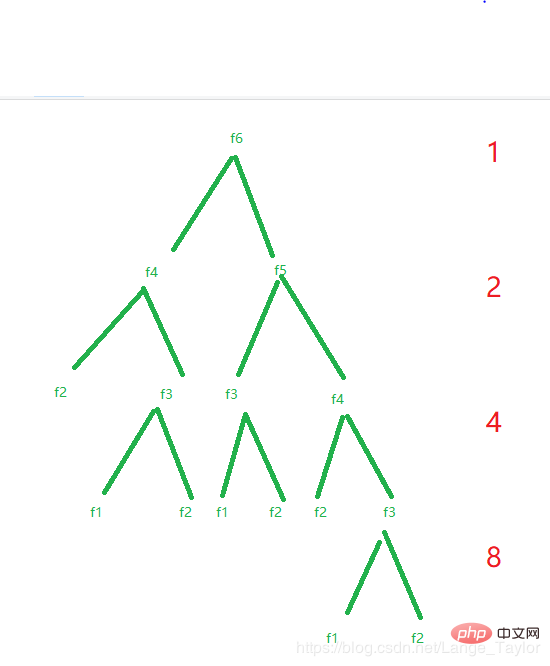计算并根据O渐进表示法得出时间复杂度.

空间复杂度:O(N);递归深度乘以(每一次递归的空间占用{有辅助空间或常量})

伪递归优化:long long fib (long long first, longlong second, int N) {if(N <3)return 1;if(N == 3)return first + second;return fib(second, first+second,N-1);}时间复杂度:O(N);递归深度乘以每次递归的循环次数空间复杂度:O(1)或O(N)关键看编译器是否优化,优化则为O(1)否则O(N);

循环优化:long longFib(int N) {long long first = 1;long long second = 1;long long ret = 0;for (int i = 3; i <= N ; ++i) {ret = first + second;first = second;second = ret;}return second;}时间复杂度:O(N);

空间复杂度:O(1);

9.常见时间复杂度

常见的算法时间复杂度由小到大依次为：　　Ο(1)＜Ο(log2n)＜Ο(n)＜Ο(nlog2n)＜Ο(n2)＜Ο(n3)＜…＜Ο(2n)＜Ο(n!)　　Ο(1)表示基本语句的执行次数是一个常数，一般来说，只要算法中不存在循环语句，其时间复杂度就是Ο(1)。Ο(log2n)、Ο(n)、Ο(nlog2n)、Ο(n2)和Ο(n3)称为多项式时间，而Ο(2n)和Ο(n!)称为指数时间。

以上就是如何评价一个算法的好坏的详细内容，更多请关注小潘博客其它相关文章！