回归分析公式推导（小白必掌握的回归分析五个步骤）

原标题：回归分析公式推导（小白必掌握的回归分析五个步骤）

这章比较难，要注意把握核心概念

【一元回归模型】

一、一元线性回归模型

yi=α+βxi+ui（就是初中学的y=kx+b）

1、其中ui是随机项，每个ui均为独立同分布，分布服从正态分布的随机变量

2、e（ui）=0，v（ui）=σ^2=常数

3、随机项ui和任意观察值不相关（cov（ui，xj）=0

记住上面三个结论

二、样本回归函数

从总体中抽取一定样本，对于解释变量（自变量）x，被解释变量（因变量）y的样本观测值也可计算其条件均值，且这个均值随x而变化的轨迹，称为样本回归线。

三、可决系数（拟合优度）

回归直线和样本观察值拟合程度，就叫可决系数

公式：r^2=ess/tss=1-rss/tss=观测的得方差/估计值的方差

r^2就是看有多少点落在回归直线上。0

1、tss总离差平方和，反应全部总离差变化最好的量，

2、ess反映了tss中被y对x回归说明的部分（在样本回归线的点）

3、rss一切随机因素构成的

tss=ess+rss

四、回归参数

ols最小二乘准则

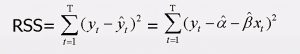
找到一个方程，最能够说明y和x关系的表达式（知识点过深，一般考得都比较简单，真得考深的，就放弃吧qaq）

【多元线性回归模型】

y=x1β1.....+xkβk+e

多个原因共同导致一个结果

一、模型假定

1、x和y具有一种线性关系

2、x之间不具有线性关系

3、随机扰动项在观察值x上的条件期望值为0，表示所有x的观察值都不能为随机扰动的期望值提供任何信息（e和前面的x没有任何关系）

4、随机扰动的方差和协方差假设，所有随机扰动的方差都相等，不同的随机扰动互不相干

5、xi是非随机的（导致因变量变动的因素是确定的）

二、多元线性回归模型

y=b0+b1x1+b2x2.....+bkxx+e

三、二元回归模型

y=b0+b1x1+b2x2+e

【线性回归模型的特征】

1、引入随机误差项（e），将变量用一个线性随机方程来描述

2、线性回归模型中，有解释变量和随机误差项共同决定的

【非线性模型的线性比）

1、非线性模型线性化的经典例子：

y=（e^β1）（x2^β2）（x3^β3）（xk^βk）(e^epsilon）

两边同时取对数

iny=β1+β2inx2+....

2、非线性回归模型的分类

1）x和y不存在线性关系，但是未知参数之间存在线性关系的非标准线性回归模型

2）x,y，未知参数之间都不存在线性关系的可线性化的非线性回归模型

3）x,y，未知参数之间都不存在线性关系的不可线性化的非线性回归模型

【回归模型常见的问题】

首先记住常见问题的名字（多选题）多重共线性，异方差问题，序列相关性模型（自相关模型）

其次记住这些问题的概念、原因、影响和解决办法（概念和原因最重要）

一、多重共线性//说的x之间的问题

1、概念：多重共线性：解释变量（x）之间存在相关关系，有一定程度的共线性，近似共线性

2、原因：1）滞后变量的引入（历史累积，每期都会对下一期有影响，自变量之间存在近似相关）

2）样本资料的限制（就是样本不足）

3）经济变量相关的共同趋势（经济繁荣的时候，企业扩展，收入上涨，消费上涨，投资上涨，这些变量之间本身就有相关关系）

3、影响，参数估计量不存在了，ols估计量非有效，参数的经济含义不合理、、、等等，反正就是那个没用了

4、解决办法：排除引起共线性的变量、差分法、减少参数估计量的方差（了解）

二、异方差问题说的μ的方差的问题

随机误差项的方差不是常数二是随机项（本应都是相等的）

原因：漏了某些解释变量，函数有问题，样本数据测量有误差，随机因素的影响（选坏的就行，全选）

影响：无偏性、有效性、显著性检验都有影响（选坏的）

三、序列相关性（自相关）说的μ之间的问题

原本应该随机误差项之间不相干，cov（ui，uj）=0

但是如果随机误差项之间有关系，就会出现这种错误

例子：消费习惯，一个人的消费习惯如果是随机误差项，但是这个跟每个人的经历有关系，所以这个回归里的随机误差项就是相关的

影响：参数估计量，显著性检验、模型预测失效（选坏的）

解决办法：首先用ols对模型估计，获取随机干扰项的近似估计量，然后通过这些近似估计量的相关行，判断随即误差项是否具有序列相关性。（ols就是找到回归方程的那个方法）

检验办法有：图示法、回归检验法、拉格朗日乘数法、杜宾=瓦森检验法（dw检验）

dw检验，在du