年金终值公式（手把手教你如何计算现值和终值）

原标题：年金终值公式（手把手教你如何计算现值和终值）

百度百科解释：年金（annuity）是指一定时期内每次等额收付的系列款项，通常用a来表示。

mba智库解释：年金（英语：annuity；德语rente），是指每隔一定相等的时期，收到或付出的相同数量的款项。

从两者解释上，智库的解释更准确些，百度解释中没体现出每次支付的间隔要相等。

通俗讲，年金就是个周期性的等额支付概念，孤掌难鸣，支付需要交易双方，一方支付，一方收款。

现值和终值，赋予了时间的约定，就天然地结合了资金时间价值的概念。

没有时间价值的基础，也没有现值和终值的区分，年金现值终值的换算就是个小学生题目。赋予资金时间价值后，年金、现值、终值的换算就陡然变成了中学生题目了。

年金数列本质上都是等比数列，不考虑资金时间价值时，比值为1，考虑资金时间价值后，比值变为（1+i），i间隔周期（通常是年）的利率值。

现值、终值又都是个年金求和的概念，所以先列出等比数据的求和公式：

公比q≠1时：

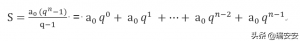
等比数据求和公式

首先说：终值的计算，根据年金求终值使用本公式时重点注意以下几点：

1. 公比q=1+i i就是利率值

2. 周期数n是年金发生的次数

3. 数列首项，

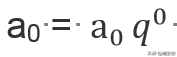
数列首项

对于数据首项引起的说明：

1） 套用在年金中，就是有一次的年金是只计本，没有利息的。因此首项只能是和终值同一个时间点的年金。

2） 这样的话，公式中的等比数据是按年金周期倒序排列的，数列中的首项对应第n次年金，数列中的第n项对应着第一次年金。

3） 再次强调，年金求终值时，在终值时间点上同样要支付年金

看图：

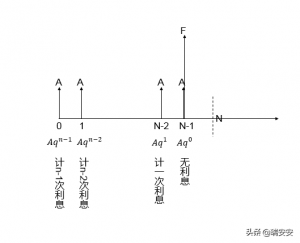
年金终值发生说明

本图是按年金在期初投入，如果想在期末投入，也是一样的，本期期末等于下期期初，只是向后移动一个周期还是这样。

年金终值公式就出来了！！

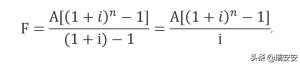
年金求终值公式

再根据现值终值公式：

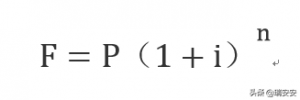
现值求终值公式

就可以进行各个值的换算了

这两个公式为什么能互相换算呢，前提条件就是计息周期相同；周期数n相同；利率i也是相同的。

另外，大家可能觉得在年金终值换算时是年金发生n次，对应周期数是n-1次，而不是n次。这儿就涉及现值、年金、终值发生的逻辑关系：现值和第一次年金相隔一个周期，终值和最后一次年金是同一个时间点。