普通年金终值计算器（年金保险复利计算公式）

原标题：普通年金终值计算器（年金保险复利计算公式）

递延年金是年金的一种具体体现形式，性格上属于“慢三拍”，现在计划，多期后才实施，不过只要一发生，就会持续有限的几期，并且会严格遵守“金额不变，发生间隔不变”的年金铁律，所以它是一个慢性子。

生活中，有很多这样的例子，比如买房贷款，现在房价不稳定，等等再说，计划三年后贷款买入房子，每月支付给银行等额本息，这就是一个递延年金，递延一段时间后才发生。

从现金流量图来看，它主要体现为：

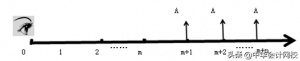
在具体运用中，主要解决两个问题，现值和终值的计算：

（1）现值计算

要计算现值，必须确定关键参数递延期（m），递延期是指相对于普通年金第一期年金发生时点（第一期期末）而言，递延年金的第一期年金发生时点的间隔期数。如某个递延年金的第一期年金发生在第5期期初，那么它的递延期应该是3期（思考一下~~~）；

在现值计算中，最为简单的方法是，先计算普通年金现值，然后再往前折现（此时的现值点为0时点，即第一期的期初），图示如下：

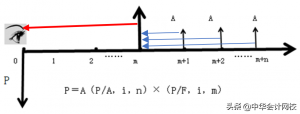
在项目投资决策中，可能会涉及该计算思路，如某项目建设期3年，运营期5年，运营期每年的营业现金净流量为200万，计算营业现金净流量的现值和，这就是一个典型的递延年金求现值的问题。

（2）终值计算

对于递延年金的终值，用得相对较少，难度也较低，需要解决的问题是：

1.终值点的确定；2.年金个数的确定。

其计算思路如图所示：

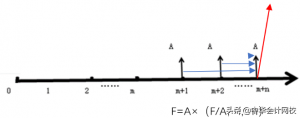
①终值点

一般默认为最后一期年金发生的时间点，即计算出来的各期年金的价值之和，其实是在最后一期年金发生时点的价值和。

②年金个数

此时年金的个数（n）和终结点的期初并不一致（m+n），此时的递延期对于终值的计算没有任何的影响。计算思路和普通年金一样，没有实质区别。

有了以上的基本思路，请同学们解决如下问题：

某公司向银行借入14873元，年利率为10%，从第5年至第10年分6次等额偿还本息，每年末偿还本息（　）元。——5000元

某公司向银行借入一笔资金，需要在第10年年末一次性偿还20000元，年利率为10%，从第5年至第10年每年年末等额存入银行（　）元，才能在第10年年末达到还款数额。——2592元。