什么是海森矩阵（海森矩阵的定义）

在高等数学中，海森矩阵(Hessian Matrix)也叫黑塞矩阵，它是由多元实值函数的二阶偏导数组成的方块矩阵。而且海森矩阵本身也包含了大量的数学知识，例如泰勒展开、多元函数求导、矩阵、特征值、特征向量等。其中，海森矩阵的特征值、特征向量是我们分析海森矩阵要重点关注的。

海森矩阵在图像处理中有广泛的应用，比如图像增强、边缘检测、特征点检测(SIFT、SURF、FAST)等。海森矩阵在图像增强方面，则是通过其特征值的绝对值大小表示图像中局部灰度的变化，特征向量表示该局部灰度变化的方向。因此，根据海森矩阵的特征值、特征向量，就可以有目的地对图像中的一些局部特性进行增强，使得我们感兴趣的图像特征变得清晰。海森矩阵在其他应用的分析方法与图像增强的分析类似，因此掌握海森矩阵在图像增强中的分析方法是很重要的。

海森矩阵的定义

在高等数学中，将一个一元函数f(x)在x0处进行泰勒展开，可以得到以下公式。

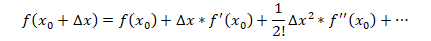
然后将其二阶导数部分映射到二维以及多维空间就是海森矩阵(Hessian Matrix)。在二元函数中，假设存在一个二元函数是f(x, y)，那么将f(x+dx,y+dy)在f(x0, y0)处展开,得到如下式子：

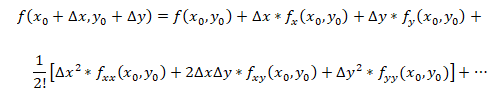
如果将上述式子用矩阵表示，并且舍去余项，则得到以下式子。

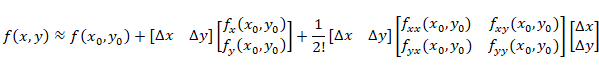
上面等式子中由二阶偏导数组成的矩阵就是一个二维空间的海森矩阵了。其表示形式如下。

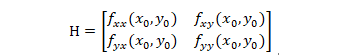
因为二阶混合偏导数fxy(x0,y0)=fyx(x0,y0)，所以海森矩阵具有HT=H的性质。因此，海森矩阵H是一个实对称矩阵。

海森矩阵的性质

从海森矩阵的表示形式中，不难看出海森矩阵是一个实对称矩阵，因此在二维图像中海森矩阵是一个2X2的实对称矩阵。由实对称矩阵的性质知，海森矩阵H的不同特征值对应的特征向量是正交的，特征值都是实数，特征向量都是实向量。对于2X2的实对称矩阵A来说，若A≠kE(k为不为0的常数，E为单位矩阵)，则矩阵A有两个不同的特征值和对应的正交向量；若矩阵A=kE，此时矩阵A的两个特征值相等，特征向量为任意不为0的二维实向量。因此，2X2的实对称矩阵一定具有两个正交的特征向量，所以二维图像的海森矩阵也一定具有两个互相正交的特征向量。

相关的证明：设2X2实对称矩阵A=[a , c ; c , b],则令|A-rE|=(a-r)(b-r)-c^2=0那么，r^2-(a+b)r+ab-c^2=0；判别式∆=(a+b)^2-4(ab-c^2)=(a-b)^2+4c^2;若方程的解r是同根，则∆=(a-b)^2+4c^2=0 ↔ (a-b)^2=-4c^2;因为c是实数，所以有c=0,a=b;因此A有两个相同特征值的充要条件为A=kE,则当A≠kE时A有两个不相同的 特征值。

如下图所示，利用MATLAB代码生成2X2实对称矩阵特征值与特征向量的性质图。其中，图1是A≠kE时的性质图，图2是A=kE时的性质图。

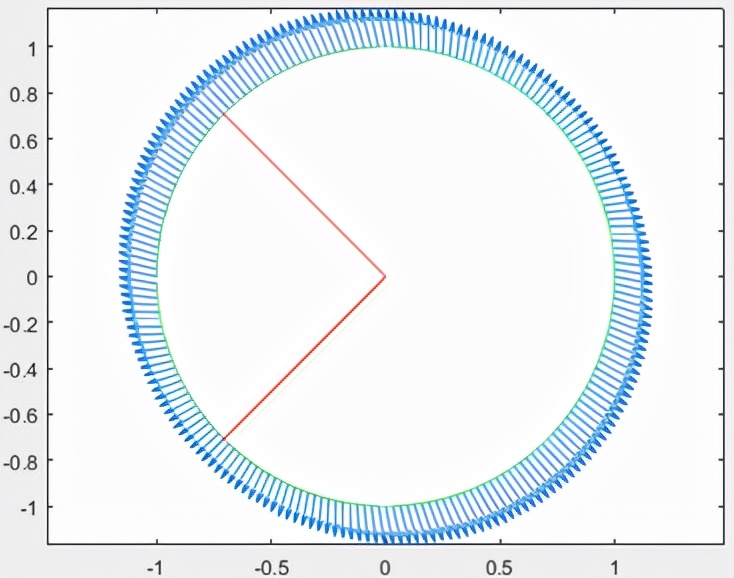
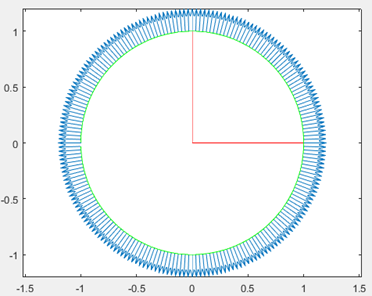
上图中绿色的那一圈是单位圆，单位圆上的每个位置和原点的连线会形成一个单位向量e，用矩阵左乘这个向量e就会得到图中蓝色的那个箭头(箭头的长度是相对长度)。图中的两个红色的线代表矩阵的两个特征向量。

通过观察图3和图4可以发现两个单位特征向量的正交的，并且两个特征向量的位置分别对应蓝色箭头最短和最长的两个位置。也就是说，对于一个2X2的海森矩阵(实对称矩阵)H，H左乘一个任意单位向量e后得到α向量，α向量的|α|取值范围为Min{|r1|,|r2|}至Max{|r1|,|r2|}，其中当向量e为H的单位特征向量时，|α|的值取到最大或最小。

海森矩阵的意义

在特定方向d上的二阶导数可以写成dTHd。当d是H的一个特征向量时，这个方向的二阶导数就是就是对应的特征值。对于其他的方向d，方向二阶导数是所有特征值的加权平均，权重在0和1之间，且与d夹角越小的特征向量的权重越大。最大特征值确定最大二阶导数，最小特征值确定最小二阶导数。

根据图像灰度梯度知识，我们可以知道二阶导数越大，灰度梯度变化得越大，因此在某个方向上的二阶导数越大，这个方向上的灰度梯度变化就越大，从而这个方向上的亮度突变越大。如果方向二阶导数越小，则这个方向上的灰度梯度变化不明显，这个方向上的亮度变化具有线性性。

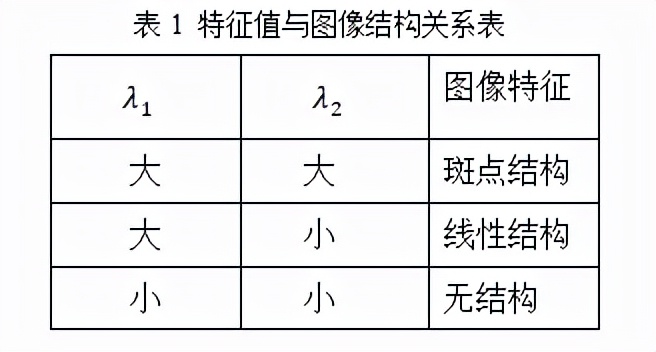
根据特征值与方向导数的关系，总结出海森矩阵两个特征值具有以下表格1的特性。

简单的应用例子

通常在数字图像中，二阶导数可以使用二阶差分来表示。

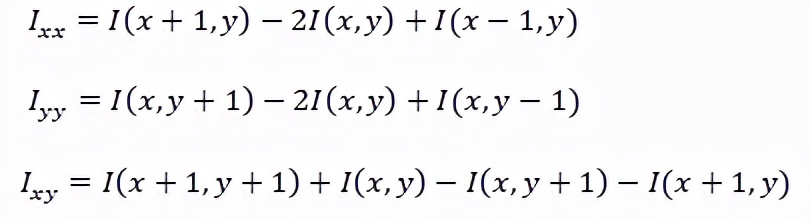
所以二维图像的海森矩阵H的描述形式为：

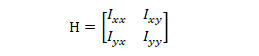
在实际应用中，这种方法的鲁棒性很差，容易受噪声干扰。同时，虽然这二阶差分公式能用来表示数字图像中某个位置的二阶变化率，但是它表示的范围太局部了。因此，根据尺度空间理论，二阶导数可以通过图像与二阶高斯模板的卷积获得。例如，在点(x,y)处的二阶导数为：

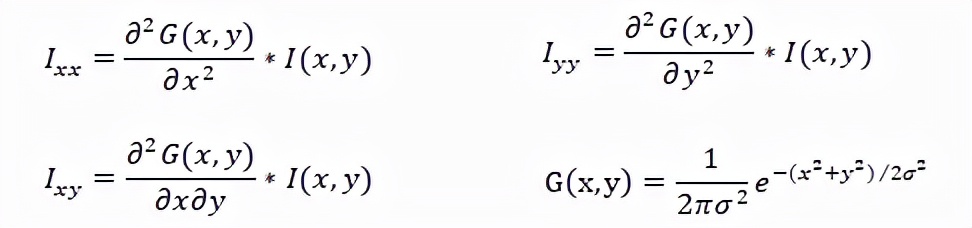
通过前面的理论分析，利用VS2019+OpenCV3.45+C++实现基于海森矩阵的图像增强算法。其中，OpenCV是一个开源的图像处理算法库。在算法实现中我们用到了OpenCV3.45算法库的cv::imread()图片读取函数、cv::imshow()显示函数、cv::filter2D()卷积函数、cv::getStructuringElement()自定义核函数、cv::morphologyEx()通用形态学函数和cv::eigen()函数计算矩阵的特征值与特征向量。实现步骤如下：

第一步，读取单通道图像，即灰度图；

第二步，生成高斯二阶偏导数；

第三步，将灰度图像与高斯二阶偏导数模板卷积；

第四步，构造海森矩阵，求特征值与特征向量，然后根据特征值判断图像中的结构，最后对判断出的结构进行增强；

第五步，对图像进行闭关操作，即先对图像进行膨胀，然后对膨胀结果进行腐蚀；

第六步，显示结果。