圆柱的表面积怎么求_求圆柱表面积简便方法

圆柱的表面积的计算和实际应用技巧讲解，收藏

圆柱表面积的计算和实际应用相结合的题型是同学们在学习圆柱相关知识当中比较复杂的内容之一，也是同学们最为困难的部分。并不是掌握了表面积的计算公式和方法就可以解决实际的问题。它需要同学们对实际的情况进行分析清楚之后，才能根据实际的要求和情况来决定表面积的计算当中涉及到地面都有哪些，然后再根据公式进行计算。

首先唐老师带大家看一看圆柱表面积的计算都有哪些重要的知识点？这是解决圆柱表面积计算的关键部分，其中蕴含的表面积计算公式是大家解决问题的基础内容。

1.沿圆柱的高剪开，圆柱的侧面展开图是一个长方形（或正方形）。（如果不是沿高剪开，有可能还会是平行四边形）

2.圆柱的侧面积＝底面周长×高，用字母表示为：S侧＝ch。

3.圆柱的侧面积公式的应用：

（1）已知底面周长和高，求侧面积，可运用公式：S侧＝ch；

（2）已知底面直径和高，求侧面积，可运用公式：S侧＝πdh；

（3）已知底面半径和高，求侧面积，可运用公式：S侧＝2πrh

4.圆柱的表面积：

S表=2S底+S侧=2πr²+2πrh

5.圆柱表面积的计算方法的特殊应用：（重点）特殊应用及结合实际情况分析清楚表面积计算当中到底有哪几个面。

（1）圆柱的表面积只包括侧面积和一个底面积的，例如无盖水桶等圆柱形物体。

（2）圆柱的表面积只包括侧面积的，例如烟囱、 油管等圆柱形物体。

在圆柱表面积的计算过程当中，首先我们要对圆柱的表面积组成有充分的了解。其主要包括上下两个底面和一个展开的侧面积，此时表面积计算有两个底面圆面积与侧面积之和组成。

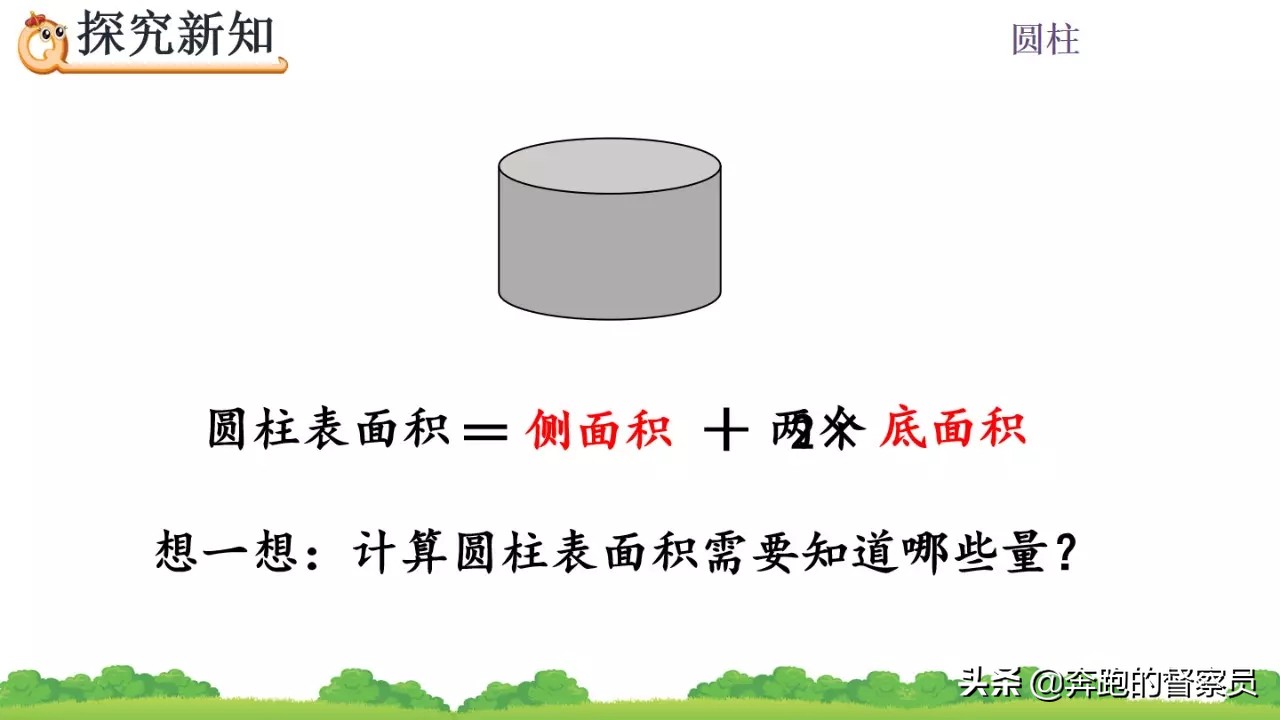
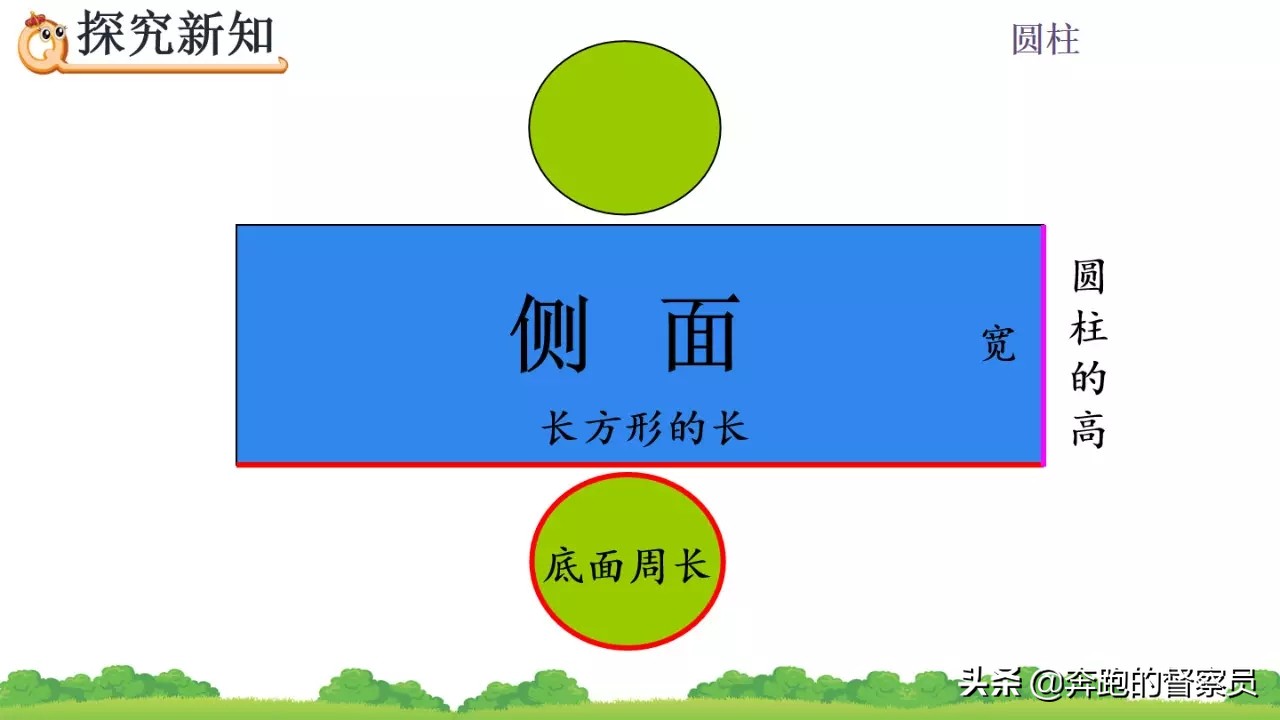
掌握圆柱的表面积计算的公式之后，对于常规的圆柱求其表面积，其主要的量需要搞清楚底面圆的半径和圆柱的高度即可进行最后的计算，所以在涉及到求表面积的题型当中，条件的挖掘主要依靠这两个量来进行，这是提高大家解题效率的关键因素。

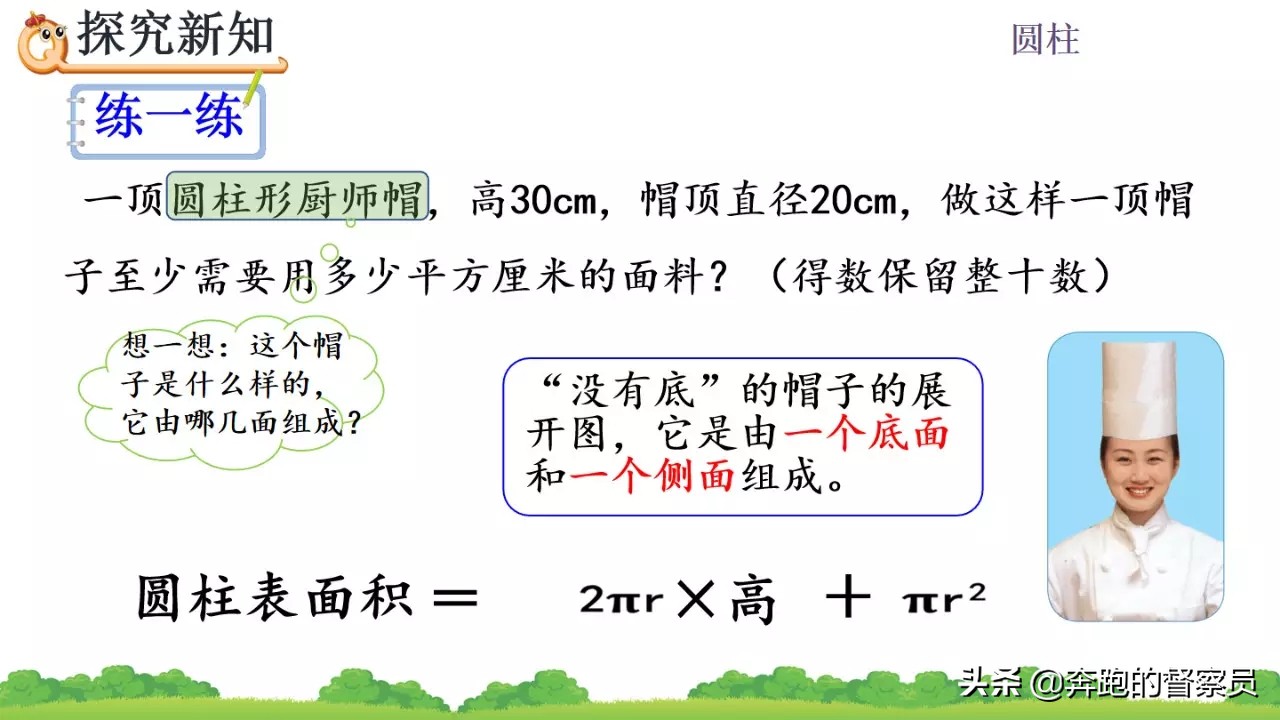
通过对圆柱展开图和表面积计算的总体分析，在进行实际的计算时，只要搞清楚两个关键的量，那么其计算还是比较简单的，以下我们将通过经典的常考题型来给大家做详细的分析，看在实际的计算当中都有哪些需要注意的地方。

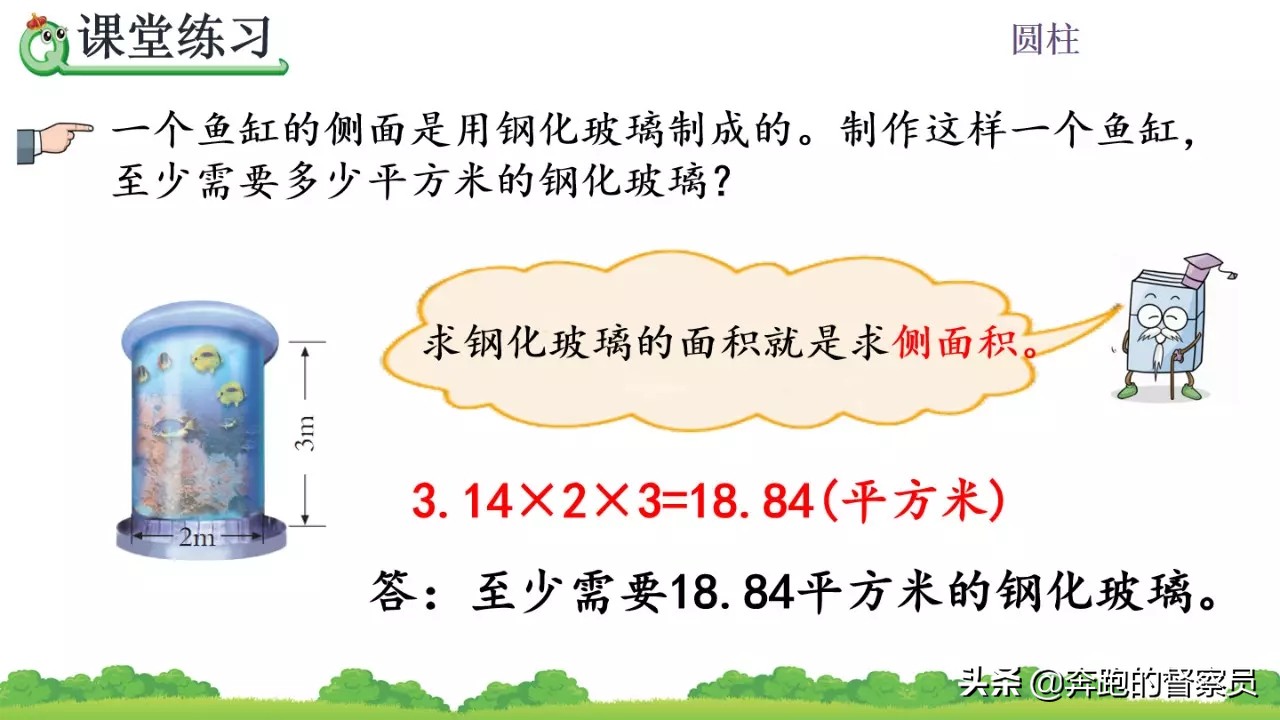
其次，在实际的问题解决过程当中，有关求圆柱的表面积的题型时，其表面积所包含的面积与原计算方式存在差异，这时我们需要根据实际的情况进行分析，确定其表面积包含的面都有哪些使再进行计算。比如实际情况当中出现无盖或只需要求其侧面积，求通风管道表面积时，其表面积也会产生相应的变化。

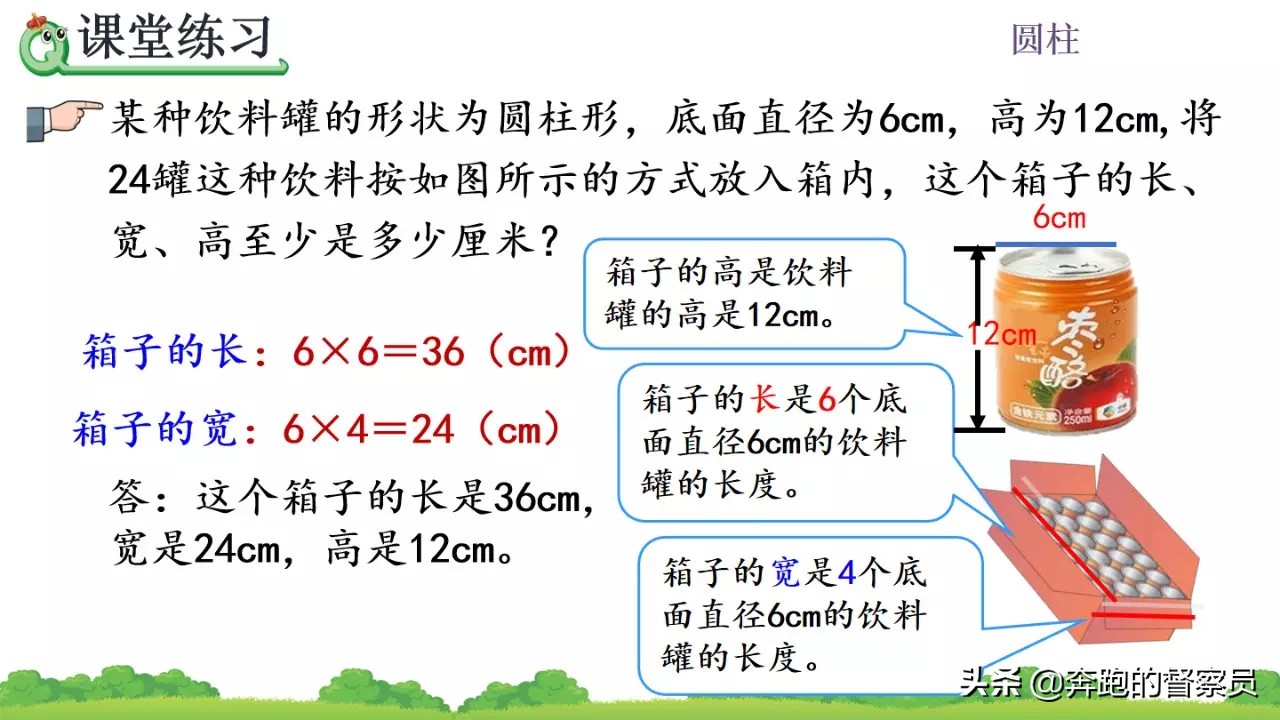
通过以上对圆柱表面积计算的实际应用和计算过程当中常考题型的解题思路的分析以及技巧的学习，我们可以通过以下的巩固学习来确定自己在圆柱的表面积计算过程当中的方法是否正确，其解题的效率是否已经满足要求。

特别是对于在实际情况中表面积计算，需要计算的面积有哪些？是大家学习过程中的难点，通过不同题型的训练才能对生活中的实际计算的例子有充分的了解。

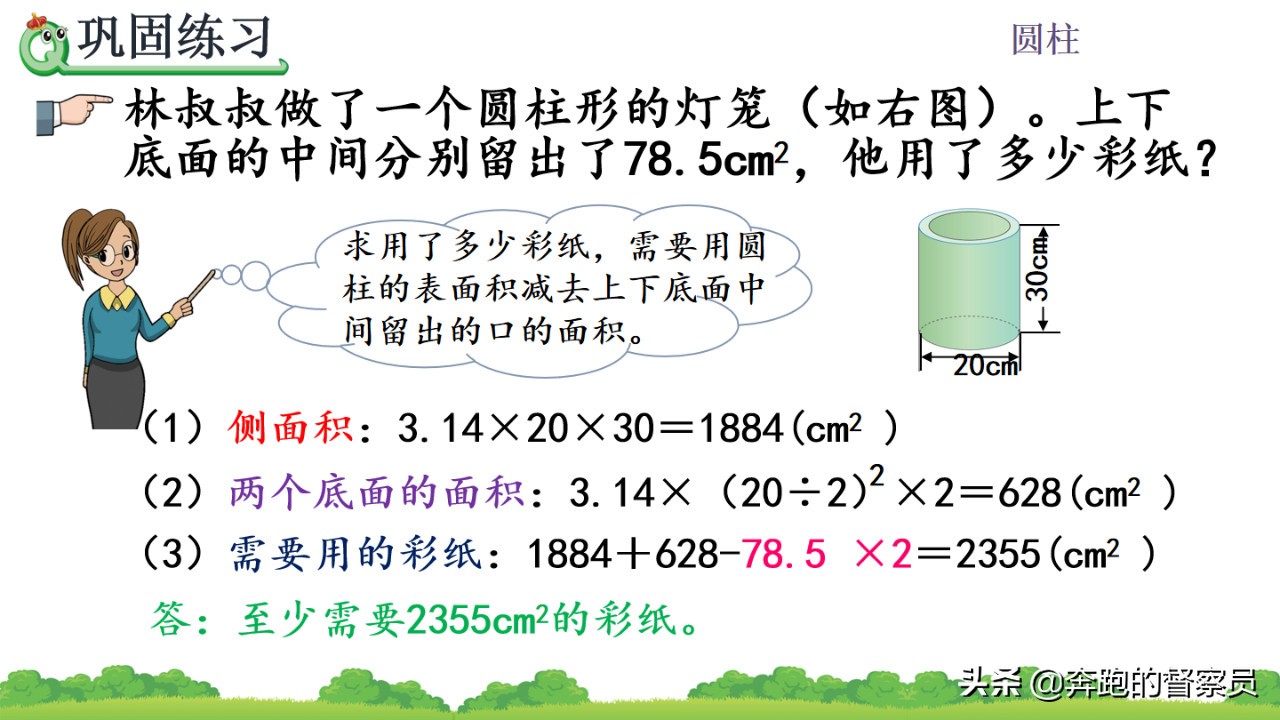
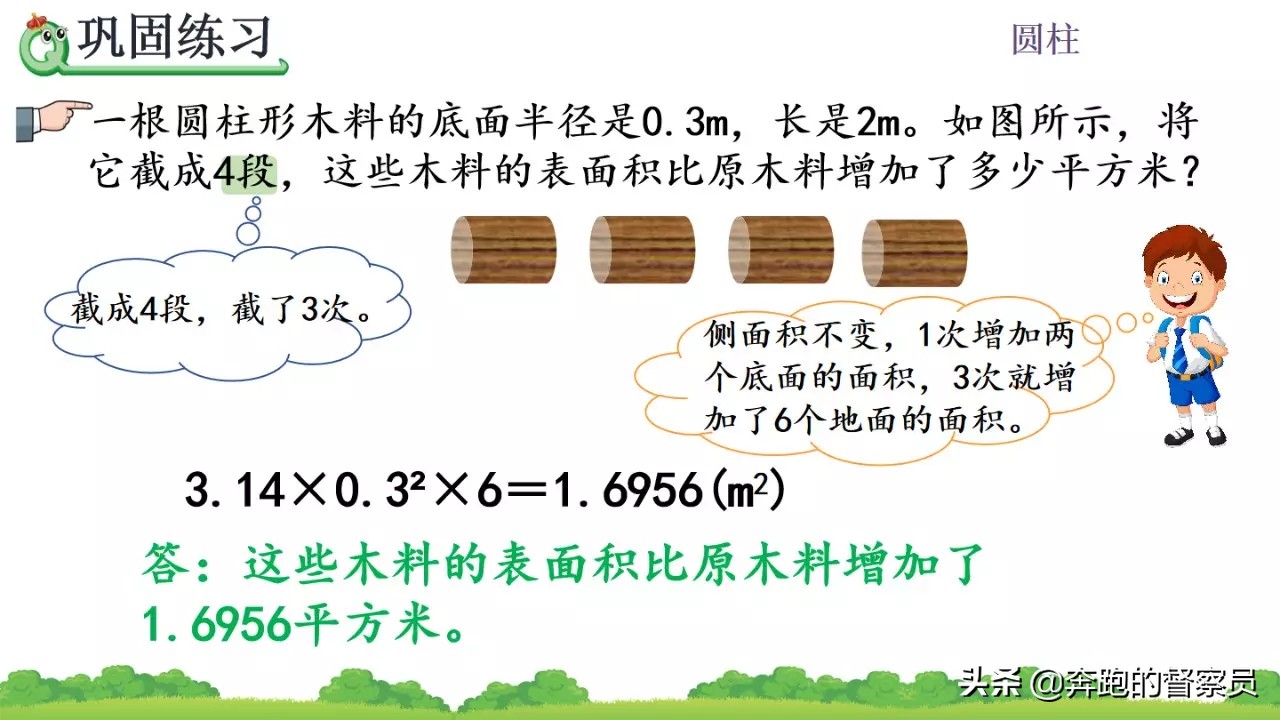
写在最后：圆柱的表面积计算这一部分主要包括了常规的表面积计算以及圆柱的上下两个底面与侧面积之和，但是在实际的运算过程当中，需要根据实际情况来确定是否需要计算三个面的面积再来进行计算，这一实际的应用需要大家对经典的题型以及常见的情况进行准确的分析。