什么是解析函数_解析函数的讲解

在欧拉的时代，变量和常数通过算术运算、三角运算、指数和对数运算构成的表达式，被欧拉称为“解析函数”。此外，欧拉考虑了“表示随意地画出的曲线的函数”，并称之为“随意函数”。在欧拉的时代，函数的概念由积分而进一步推广。即：考虑任意的解析函数f(x)，其积分

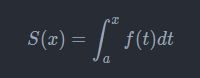
表示的式子，表示f(x)和与y轴平行的两直线及x轴所围图形的面积，而这种反映几何关系的S(x)$也可定义为函数，但这种函数就不一定是“解析函数”。

3类曲线

函数的范畴由“解析函数”扩充到几何学上的函数。在那个时代，几何学中的曲线被分为3类：

第一类，能用一句话表明曲线本质或一个表明曲线本质的等式来定义；例如圆的本质，曲线上任一点到一定点的距离为常数； 第二类曲线，不能用一句话或一个等式表明其本质； 第三类曲线，由两条以上的第一类曲线构成的曲线。 在上述3类曲线中，第一类总能用一个解析式y=f(x)或F(x,y)=0来表示，而其余的曲线不能由一个解析式表示。因此，把表示第一类曲线的解析式看作“连续函数”或“真函数”，其余函数为“伪函数”。在这样的背景下，人们对于函数还有以下的一些认识：

事实上，上面的认识几乎全部都是错误的！这对那个时代的人来说，绝对是颠覆性的。他们做梦也没想到：任意曲线都可用周期函数表示；可用一个式子来表示不连续的线；两个函数在一个区间上恒等，并不意味着在区间之外也相等。而这几个谬误，都由傅里叶发表的“能用三角函数的级数表示函数”的论文而一一指出。

傅里叶的纠正

1807年，傅里叶发表题为《热的分析理论》的论文，论文中证明了“由不连续的线给出的函数，能用一个三角函数式来表示”。例如下面的分段函数，用3个式子表示：

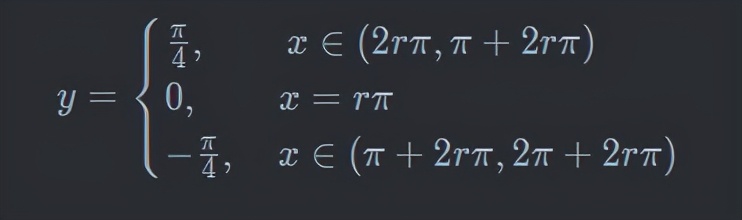
其中，r为整数。

【傅里叶的第一个纠正】傅里叶证明了，上面这个不连续的线，可唯一地用一个式子

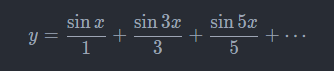
来表示。由此可知，该不连续线既可以用一个式子表示，也可用多个式子表示。因此，“能否用一个式子表达”是不能作为判别“真函数”和“伪函数”标准的，这也是傅里叶对函数概念的第一个贡献。

【傅里叶的第二个纠正】方程y=π/4表示一条与x轴平行的直线，该直线与

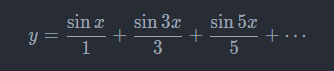
所表示的线，在区间(0,π)上是重合的，但在区间(π,2π)上，却是没有交点的。该事实清楚地表明，当时世人对函数的这种相等的认知是荒谬的。

【傅里叶的第三个纠正】根据傅里叶的研究，不仅周期函数，任意的连续函数f(x)，在-π<x<π的范围内，都可以用正弦、余弦这样的周期函数来表示。这也是最出人意料的一点，当时的数学家所完全未能考虑到的。

傅里叶的研究表明，关于函数的传统观点从根本上说都是错误的。自此之后，数学家陆续发现了同一条线既可用一个表达式，也可用两个以上的表达式表示的例子。从而使得，欧拉时代所谓的“真函数”失去了意义，也促进了柯西寻求函数新的定义。