大气压强是多少_大气压强的计算
一、液体封闭的静止容器中气体的压强
知识要点:
1.液体压强产生的原因是由于液体受重力的作用.若液体在失重的情况下,将无压强可言.
2.由于液体具有流动性,它所产生的压强具有如下几个特点
(1)液体除了对容器底部产生压强外,还对“限制”它流动的侧壁产生压强.固体则只对其支承面产生压强,方向总是与支承面垂直.
(2)在液体内部向各个方向都有压强,在同一深度向各个方向的压强都相等.
(3)计算液体压强的公式是P=ρgh.可见,液体压强的大小只取决于液体的种类(即密度ρ)和深度h,而和液体的质量、体积没有直接的关系.
(4)帕斯卡原理:密闭容器内的液体能把它受到的压强按原来的大小向各个方向传递.
3.容器底部受到液体的压力跟液体的重力不一定相等.容器底部受到液体的压力F=PS=ρghS,其中“hS”是底面积为S、高度为h的液柱的体积,“ρghS”是这一液柱的重力.所以,容器底部受到的压力其大小可能等于,也可能大于或小于液体本身的重力.
(1)液体在距液面深度为h处产生的压强:Ph=ρgh(式中ρ表示液体的密度)。
(2)连通器原理:在连通器中,同种液体的同一水平面上的压强相等;
4.解题的基本思路
液体封闭的气体的压强计算常用参考液片分析法
5.计算的方法步骤是
①选取假想的一个液体薄片(其自重不计)为研究对象;②分析液片两侧受力情况,建立力的平衡方法,消去横截面积,得到液片两侧的压强平衡方程;
③解方程,求得气体压强。
例题:如图所示,分别求出三种情况下气体的压强(设大气压强为P₀=1x10⁵Pa)。
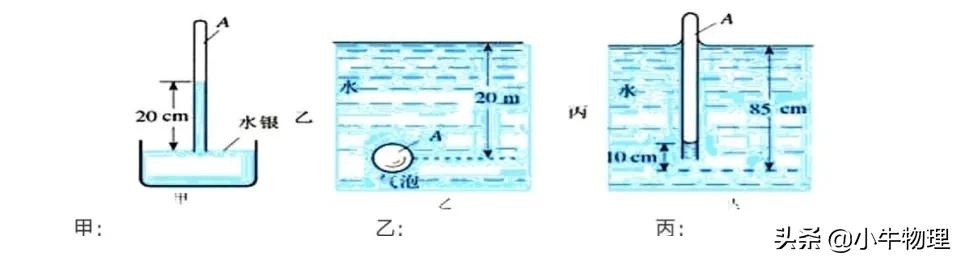
【解答】
甲:P₀S=PAS+mg
乙:P=P₀+ρgh
丙:P=P₀+P₁
例题:如图所示,玻璃管中都灌有水银,分别求出几种情被封闭的气体的压强(设大气压强为76cmHg).
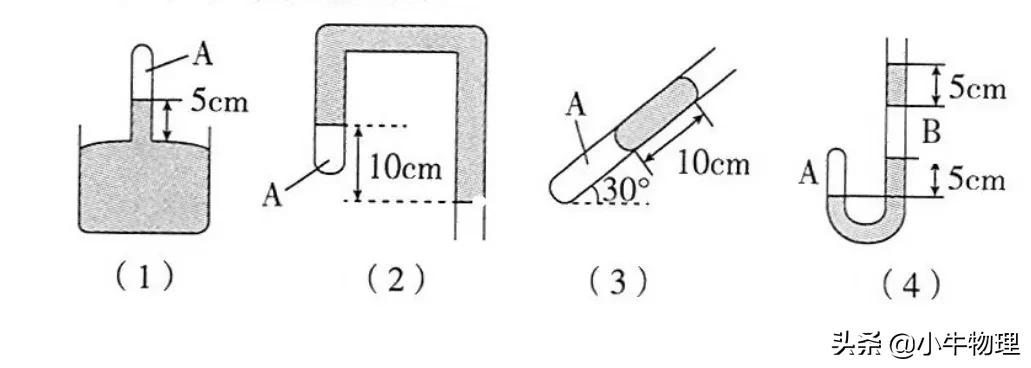
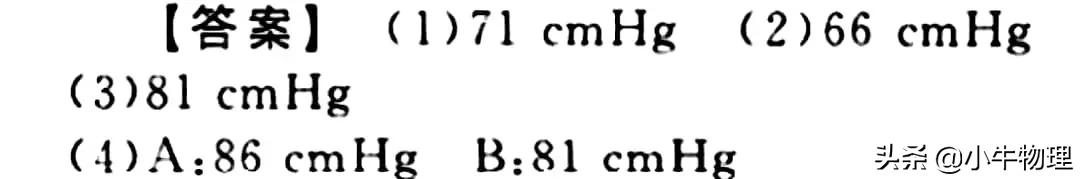
例题:如图所示,粗细均匀的竖直倒置的U形管右端封闭,左端开口插入水银槽中,封闭着两股空气柱1和2,已知h₁=15cm,h₂=12cm,外界大气压强p₀=76Hg,求空气柱1和2的压强。
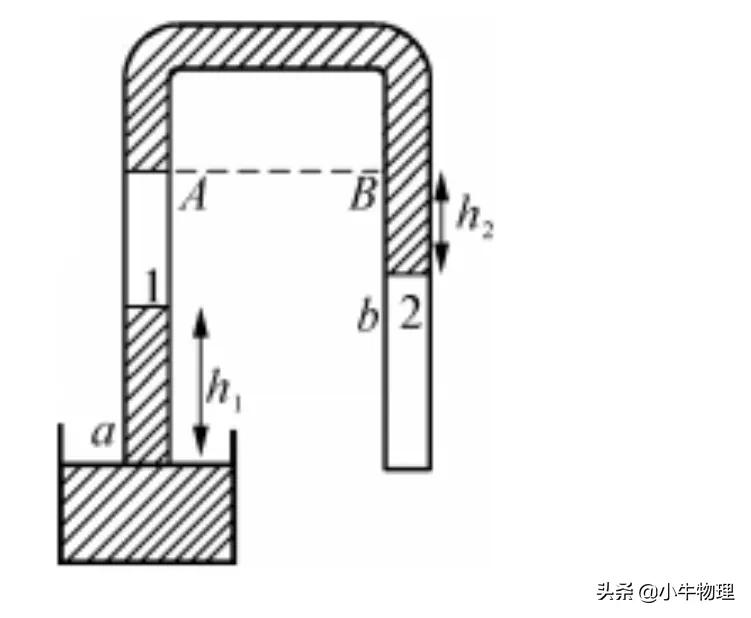
解:设空气柱1和2的压强分别为p₁和p₂,选水银柱h₁和下端管内与水银槽内水银面相平的液片a为研究对象,根据帕斯卡定律,气柱1的压强p₁通过水银柱h₁传递到液片a上,同时水银柱h₁由于自重在a处产生的压强为h₁(cmHg),从而知液片a受到向下的压力为(p₁+h₁)S,S为液片a的面积,(液片a很薄,自重不计)液片a受到向上的压强是大气压强通过水银槽中的水银传递到液片a的,故液片受到向上的压力为p₀S,因整个水银柱h₁处于静止状态,故液片a所受上、下压力相等,即(p₁+h₁)S=p₀S,故气柱1的压强为p₁=p₀-h₁=76cmHg-15cmHg=61cmHg,通过气柱1上端画等高线AB,则由连通器原理可知:pB=pA=p₁,再以水银柱h₂的下端面的液片b为研究对象,可求得空气柱2的压强为(与求p1同理)p₂=pB+h₂=(61+12)cmHg=73cmHg.
☞【解题方法提示)
求静止液体封闭气体的压强时,一般选取和气体相关液柱的最低液面为研究对象;
对液片进行受力分析,列出平衡方程分析解答。
二、活塞封闭的静止容器中气体的压强
解题的基本思路
(1)对活塞(或气缸)进行受力分析,画出受力示意图:(2)列出活塞(或气缸)的平衡方程,求出未知量。注意:不要忘记气缸底部和活塞外面的大气压。
例题:如图所示,
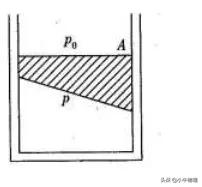
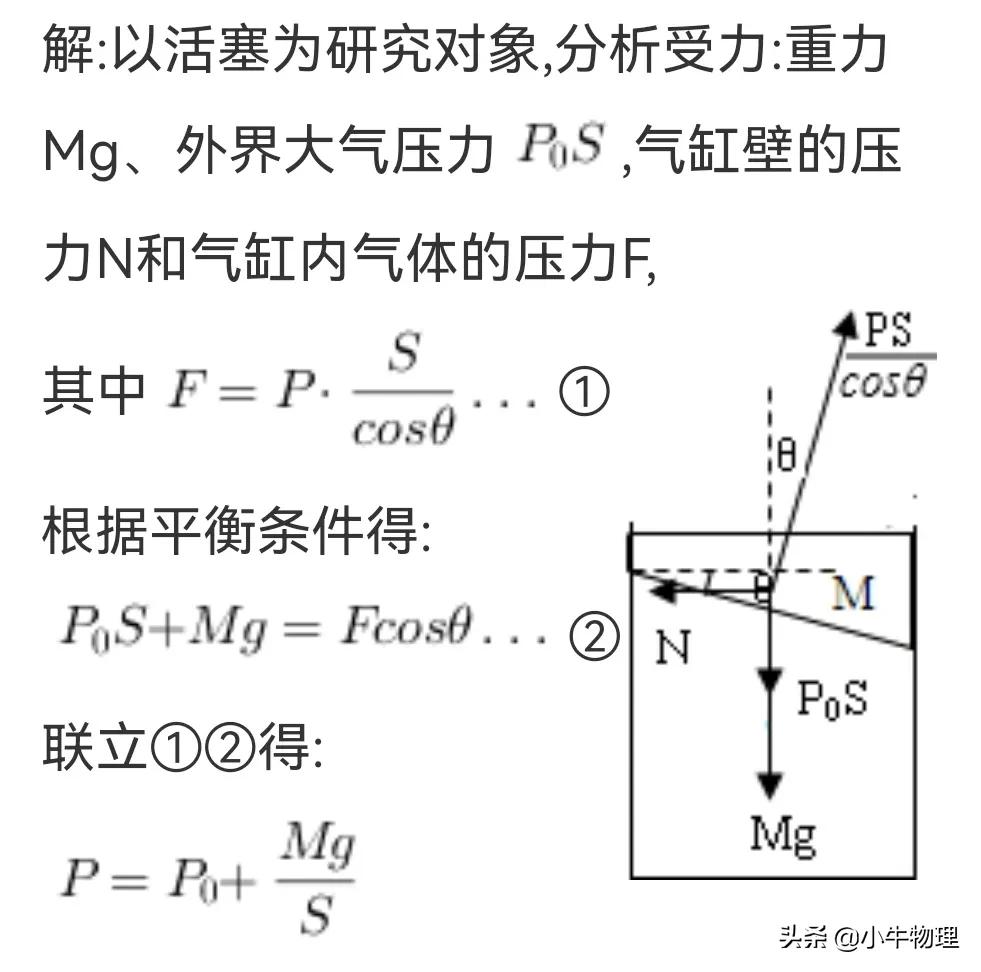
一个横截面积为S的圆筒形容器竖直放置.金属圆板A的上表面是水平的,下表面是倾斜的,下表面与水平面的夹角为θ,圆板的质量为M.不计圆板与容器内壁之间的摩擦.若大气压强为P₀,则被圆板封闭在容器中的气体的压强p等于()

三、加速运动的封闭容器中气体的压强
解题的基本思路
(1)恰当地选取研究对象(活塞、气缸、水银柱、试管或某个整体等),并对其进行受力分析;
(2)对研究对象列出牛顿第二定律方程,结合相关方程求解。
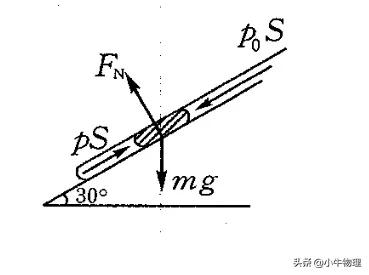
例题:如图所示,有一段12cm长的汞柱,在均匀玻璃管中封住一定质量的气体,若开口向上将玻璃管放置在倾角为30°的光滑斜面上,在下滑过程中被封气体的压强为(大气压强p₀=76cmHg)().
A.76 cmHg
B.82 cmHg
C.88 cmHg
D.70 cmHg
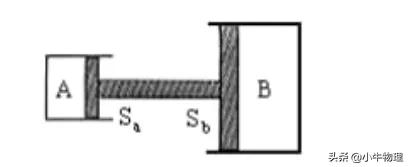
例题:如图所示,水平放置的气缸A和B的活塞面积分别为Sa和Sb,且Sa>Sb,它们可以无摩擦地沿器壁自由滑动,气缸内封有气体。当活塞处于平衡状态时,气缸A、B内气体的压强分别为Pa和Pb,(大气压不为零),则下列正确的是(BCD)
A.Pa:Pb=Sa:Sb
B.Pa>Pb
C.Pa<Pb
D.Pa=Pb


